As we enter the era of quantum utility, we’re beginning to think seriously about how to run error-free computations on large-scale quantum computers with strategies like error correction. With error correction specifically, we encode quantum information across more qubits than we’d otherwise need, using the extra qubits to help protect the information against errors.
Last year, we debuted a new way to encode quantum information into error correcting codes — one that gave us confidence in our ability to build error-free quantum computers with a lot less overhead than we previously thought.1 We call it the gross code, and it’s based on a family of codes called qLDPC codes. But there’s a challenge: it remains to be seen how to run computations on the information once we’ve encoded it.
With recent research,2 our team in collaboration with physicist Shehryar Sikander from Rutgers and mathematician Elia Portnoy from MIT has made significant progress toward answering that question. The answer lies in the realm of topology and geometry. We studied qLDPC codes where we treat the layout of the physical qubits and the information we store on them as geometric objects themselves, and explore the mathematical properties of those objects in order to unlock previously-hidden symmetries. We hope that the information gleaned from this mathematical exploration will be applicable to our gross code. But in taking this journey, we also uncovered profound connections between the behavior of our qubits arranged in quantum codes and matter itself.
qLDPC codes
At the most basic level we build redundancy into our qubits to protect against errors by using more physical hardware to represent our information than we’d otherwise need. Thinking about the most-naive example on classical bits for a second, you might use three physical bits to represent one bit of information, where at least two bits set to “0” represent the “0” you use to compute with, and at least two bits set to “1” represent a “1.” Quantum error correction relies on a similar concept though with more structure to account for the extra information stored in quantum bits.
Today, the leading family of error correcting codes are called quantum low-density parity check (qLDPC) codes. The main advantage of such approaches is that they require fewer extra qubits to do error correction than more conventional codes as we scale them up. We can measure the overhead as a ratio between the number of physical qubits we encode our information into, n, and that of the logical qubits that represents our information, k. In the example above, the ratio is n-to-one. This ratio can approach a constant number in qLDPC codes. Another important quantity which has nice scaling in the qLDPC code is the code distance, meaning the number of qubits the errors can corrupt without destroying the underlying information. In the above example, the distance is 3. Any more errors than half — in this case, 2 or more errors — and you would flip the logical bit value.
So, what’s the challenge with these new codes?
Well, while qLDPC codes offers an efficient way to encode quantum information, we still need to figure out how to run operations on that encoded information. But the challenge is two-fold:
-
First, for these qLDPC codes, all of the logical information is spread out among all of the physical qubits collectively — so you couldn’t draw a 1-to-1 map describing which physical qubits are responsible for storing which pieces of quantum information as we do above. Because of this encoding, standard ways of running logical gates would only be able to address all of the qubits at the same time, rather than a subset.
-
The second issue is that so far, the only logical gate operations for qLDPC codes are a set of logical Clifford gates. But theory says that these gates can already be efficiently simulated on a classical computer, so we don’t get a meaningful computation advantage by using them. To perform universal quantum computation which can have advantage over classical computation, one also needs to implement logical non-Clifford gates on these codes. The only way we knew how to run these gates on our codes are through a protocol called magic state distillation, which can consume a lot of extra space-time resources.
A recent work2 by IBM researchers and collaborators has made some significant progress on solving both problems through a deeper mathematical understanding of qLDPC codes, and the underlying symmetry and geometry
Donuts in hyperspace
Error correcting codes are essentially rules for how you spread your information out across the qubit layout. In order to address this challenge, we needed to consider our qubit layout differently — including the very space they exist in.
Today’s conventional codes, such as the famous surface code, treat the qubits in the most naïve geometrical way, where you can visualize 2- and 3-dimensional spaces with a square or a cube, and where three right turns take you back to where you started. We call this treatment of geometry the Euclidean geometry. But this isn’t the only way to visualize space — we can also imagine non-Euclidean geometries where the shape of space and the mathematics that describe it is different. We experience non-Euclidean geometry here on our spherical Earth — if you set off from the equator to the North Pole, you can return back to where you started with two right turns. You can imagine other exotic spaces, like ones where you’d need to take five right turns to get back to where you started or with other conditions.
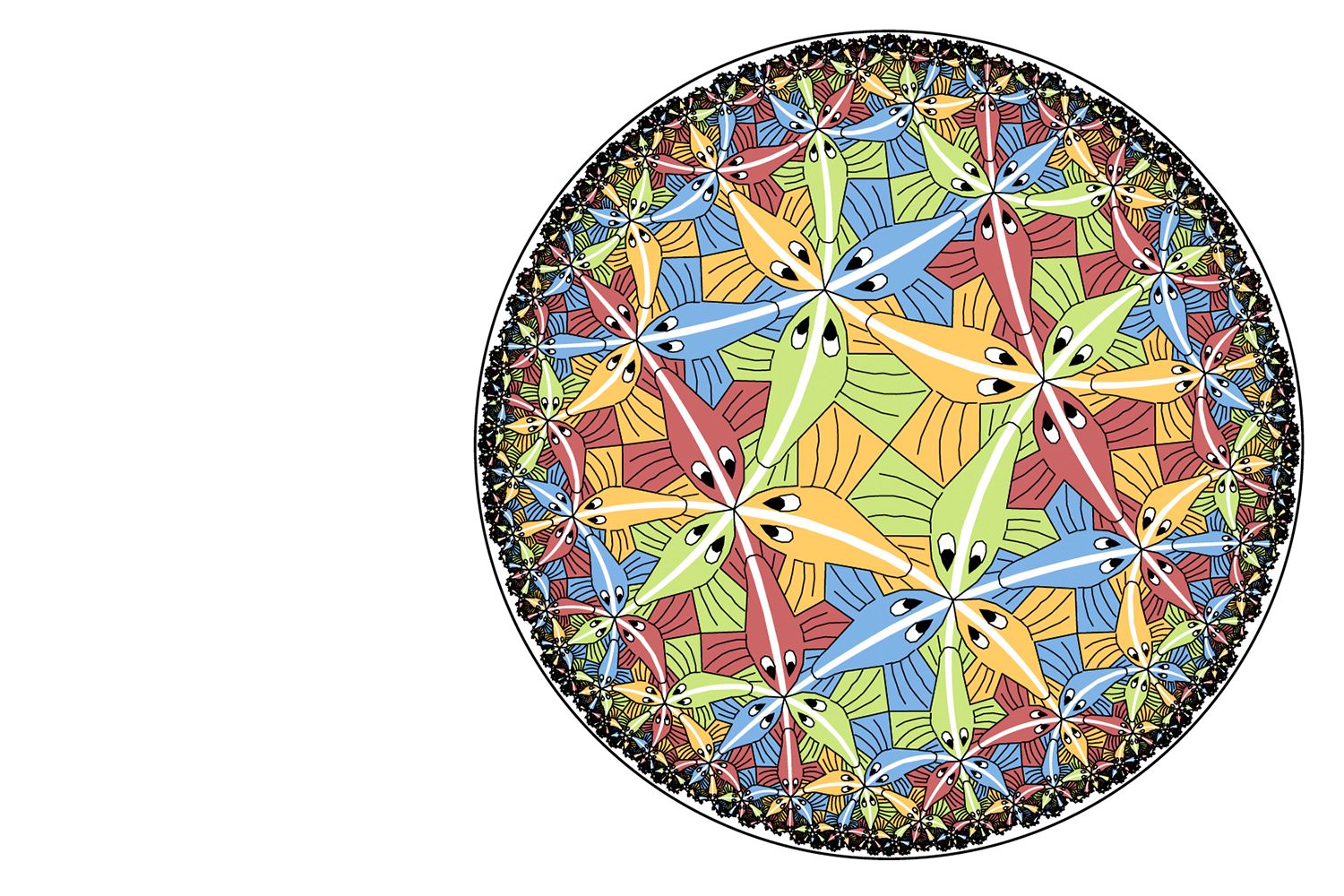
Fig. 1: M. C. Escher’s painting “Circle limit III”,3 which serves as an artistic illustration of the tiling of a Poincaré disk model of the 2D hyperbolic surface. A 2D hyperbolic code can be defined on such tiling with proper boundary conditions, where the qubits reside on the edges (white arcs) of this tiling. The geodesics are represented by long white arcs along the fish with the same color starting and terminated on the boundary of the Poincaré disk at infinity.
Embedding our qLDPC codes into non-Euclidean spaces turns out to be necessary in the age of quantum computing.
In our new work, we construct a qLDPC code by tiling qubits on an hyperbolic non-Euclidean three-dimensional space, what we call a manifold. A two-dimensional analog of the hyperbolic space and code is illustrated in Fig. 1. A manifold looks locally like a flat Euclidean space, but is globally different — like Earth. But you can dream up more exotic manifolds than Earth — they can have higher-dimensional shapes that give rise to “holes” in the space.
For instance, a torus — the shape of an inner tube — is actually a two-dimensional manifold equivalent to a square patch that has been curved such that it has special boundary conditions both horizontally and vertically. It has two “holes,” the donut hole and the hollow space inside the inner tube. Higher-dimensional tori are more challenging to imagine, since we don’t live in a higher-dimensional space — but you could imagine a 3D torus where space is warped such that you can add a third hole, where moving in any direction, up-down, left-right, and in-out, would cause you return to where you started around one of these holes, as illustrated below in Fig. 2(a).
In our paper,2 we find that we can solve our problems by constructing a qLDPC code where we tile our qubits on one of these exotic 3D spaces. In our codes, the size of those holes determines the code distance — bigger holes means a better code. The number of holes represents the number of logical qubits — more holes means more logical qubits. And the volume is proportional to the number of physical qubits. Therefore, the best code is one supported on a manifold with as many holes as possible, and where those holes are as large as possible.
The best code is one supported on a manifold with as many holes as possible, and where those holes are as large as possible.
Manifolds and submanifolds
But that doesn’t answer the question: How do we run non-Clifford gates on our qLDPC code, and how do we address the individual logical qubits, instead of all of the qubits at the same time? Well, this is the reason why we’ve gone beyond 2D manifolds. Previous work on codes called color codes has already shown that certain codes based on these higher-dimensional Euclidean geometries allow us to implement non-Clifford logical gates. Now, we’ve applied similar ideas to the qLDPC code embedded on this 3D manifold. We get all of the benefits of the qLDPC code’s scaling, plus the ability to run logical gates from those simpler color codes.
First, there’s addressing our subsets of qubits with parallelizable gates. In our code, this is equivalent to operations that act on two-dimensional subsets of this three-dimensional space — like a circle embedded in a sphere, but applied to the theoretical hole-filled warped space on which we’ve embedded our qubits. You can imagine that there are lots of different ways to slice this space, and the number of gates we have access to scales exponentially with the number of holes—the number of logical qubits.
Then, there’s running non-Clifford gates. Here, we rely on new symmetries that have emerged in constructing codes in this higher-dimensional space. You can imagine that moving from a two-dimensional world to a three-dimensional world gives you access to new physical properties — that’s what’s going on here. Here, topological defects emerge — robust physical objects that don’t change under local deformations, such as vortices in fluid or magnetic domain walls in a hard drive. Instantaneously moving these defects around allow us to run non-Clifford gates.
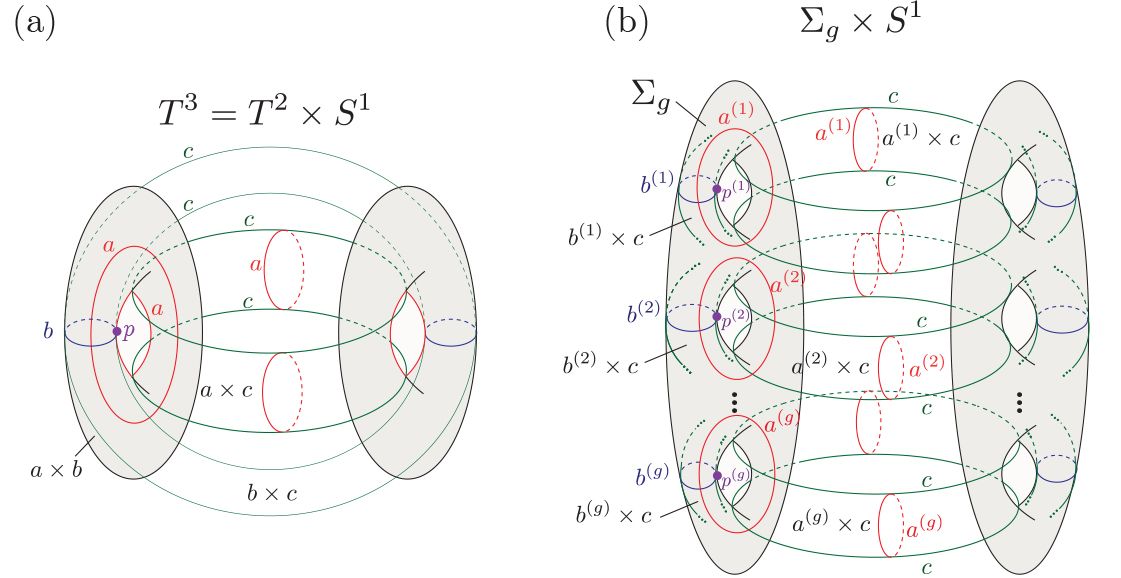
Fig. 2: From our paper,2 (a). A 3D torus can be considered as a product of 2D torus T2 and a circle S1. The non-contractible loop — the “holes” — on the 2D torus is labeled as a and b, while another “hole” along the circle is labeled as c. The Poincaré dual non-contractible membranes of the loop a, b, and c are 2D tori formed by the product of the other two loops, i.e., b x c, a x c, and a x b respectively. Each loop and its dual membrane intersect at a single point p. (b). A quasi-hyperbolic code defined on a 3-manifold formed by a product of a surface, called Σg, and a circle S1. The non-contractible loops on the surface surface are labeled as a(i) and b(i), while the loop along the circle is labeled as c. There is one non-contractible membrane supported on the surface Σg, while the other membranes are supported on tori formed by the product of two loops and labeled as a(i) x c and b(i) x c. There are g triplet of membranes a(i) x c, b(i) x c and Σg intersects at g points p(1), p(2), … p(g).
Interestingly, a quantum code supported on a 3D manifold like this turns out to be equivalent to a specific type of topological quantum field theory (TQFT). Quantum field theory is the most accurate theory describing the microscopic world, including elementary particles, light and even the vacuum that surrounds us and fills the universe. It is also powerful to describe other quantum many-body systems such as various quantum materials.
Here, it describes our quantum code, which you can think of as a many-body system formed with many qubits. Though we’ve omitted the specifics, running non-Clifford gates on our qLDPC codes is based on the same physics that governs famous quantum materials such as topological insulators, materials whose interiors act as insulators and whose exteriors act as conductors with topologically protected edge currents that have become a popular physics research area, as pointed out in the previous work by our team and collaborators at University of Maryland and Caltech.4 It’s profound that we can use the physics of quantum matter to help guide our exploration into quantum computing.
What does all this mean in practice? Well, we don’t expect our quantum processors to look like hyperdonuts. Instead, we would use short-range and long-range connectors in ways such that our qubits etched into chips represent a discrete version of these higher-dimensional shapes.
Building our codes
In our paper,2 we constructed three different families of 3D manifolds which give rise to three families of qLDPC codes, all with a constant or almost-constant overhead. The first construction takes a product of the 2D hyperbolic surface with genus g (the number of “holes” being 2g) and a circle that grows logarithmically with g. The g=1 case (a 3D torus) is illustrated above in Fig. 3(a) and the case of general g is illustrated in Fig. 3(b). The overhead — that ratio of physical storage to the logical information it encodes — scales linearly with the volume proportional to the total number of physical qubits up to a logarithmic reduction. The code distance also scales logarithmically with the total number of qubits.
The second and third construction both take an additional twist in the product and choose the length of the circle to be a constant. The difference makes the second construction also almost-constant overhead and gives the third construction constant overhead. While the second construction also has a square root logarithmic distance, the code distance of the third construction remains unknown at this moment.
The remainder of this work focuses on developing the math to further study the 3D manifold, which hasn’t been deeply explored in previous math literature. This work has hence also established a deep connection between the complexity of quantum states and the geometry or topology of the underlying manifold.
As a significant breakthrough, this work is the first study of non-Clifford logical gates in quantum LDPC codes with constant or almost-constant overhead. The discovery is based on a deep understanding of the connection between the logical gates of qLDPC codes, topology and geometry of 3D manifolds as well as the higher symmetries in the corresponding topological quantum field theory. The insight obtained in this work will also shed light on understanding logical gate structure for a more general class of qLDPC codes based on more general chain complex which are beyond the family of qLDPC codes studied in this paper, such as quantum expander codes and the gross code.
This research was funded by the U.S. Department of Energy, Office of Science, National Quantum Information Science Research Centers, Co-design Center for Quantum Advantage (C2QA) under contract number DE-SC0012704.



