The preparation of quantum states is an essential process in quantum computing, and an important first step in executing quantum algorithms. But in many cases, a quantum computer will operate only on a subset of its qubits at a given time, meaning the state of some qubits must be put “on hold” at intermediate times. In other words, if the quantum computer is working on a subset of qubits, we want to keep the other qubits in the system idle in the state we’ve prepared. This may sound relatively straightforward, but in practice, it can be a pretty challenging task.
That’s because quantum states are delicate and unstable. Once you’ve prepared a quantum state, it won’t just sit there waiting until you’re ready to proceed with your computation. Quantum computers are incredibly sensitive to environmental noise, which can lead to fluctuations or uncontrolled erasure of information in the quantum states we’ve prepared. Better, more accurate methods for modeling this noise could ultimately help us improve quantum systems, making them more resilient to the effects of noise.
In a recent paper published in Physical Review Letters and written in collaboration with our colleague Grégoire Misguich from Université Paris-Saclay, we introduce a new and improved model of the noise that acts on superconducting qubits when they are idle, and validate this model using experiments on IBM’s quantum hardware. Notably, this noise comprises both dissipative (incoherent) and coherent one-qubit components, as well as two-qubit (coherent) crosstalk of neighboring qubits, all of whose parameters are extracted from the device using the versatile Qiskit Experiments framework.
Our paper is the first to show how this noise is reflected in the continuous dynamics of specific few-qubit observables called “stabilizers,” which can be defined by certain states on which they are measured—more on these later. In our paper, we focus on graph states, whose entanglement can be abstracted using a graph structure. Our research also demonstrates how tailored dynamical decoupling can suppress noise described by this model, including in these stabilizers.
We believe our model can be a useful tool for building efficient and quantitatively accurate computer simulations of the effects of noise on quantum states comprising many qubits. In this article, we’ll provide readers with a high-level overview of the model we built and the experiments we ran. But before we do that, let’s talk a bit more about those stabilizers and why they’re so important.
The role of stabilizers in quantum computation
Stabilizers are a specific class of multi-qubit observables—quantum mechanical quantities that are shared by multiple qubits, and that can be measured via experiments. We use stabilizers widely in theoretical quantum information science because they have a rich mathematical structure that we can describe elegantly using group theory. This makes them extremely valuable, as they help us deal with quantum states and operations in a way that is simpler and more compact than alternative methods.
The noise that affects qubits manifests as decays in the stabilizer expectation values we measure. Perhaps surprisingly—since we often associate noise with the erasure of information—this noise can also manifest as a “revival” of those same expectation values. In other words, noise can cause stabilizer expectation values to decrease, but it can also cause the values to increase again, approaching their original values.
A better noise model could help us explore new methods of treating and mitigating these qubit errors. (For more details on quantum error mitigation methods, take a look at this 2022 post on the IBM Research Blog.) It could also be important to achieving the long-term goal of quantum error correction, in which stabilizers often play a central role.
Quantum error correction is an as-yet unrealized capability that will enable the quantum computers of the future to completely correct errors caused by environmental noise. Advancing capabilities to enable error correction is a central ongoing effort in IBM from theory, software, and hardware perspectives. (For more on error correction research at IBM, be sure to read our two most recent blogs on the subject, here and here.)
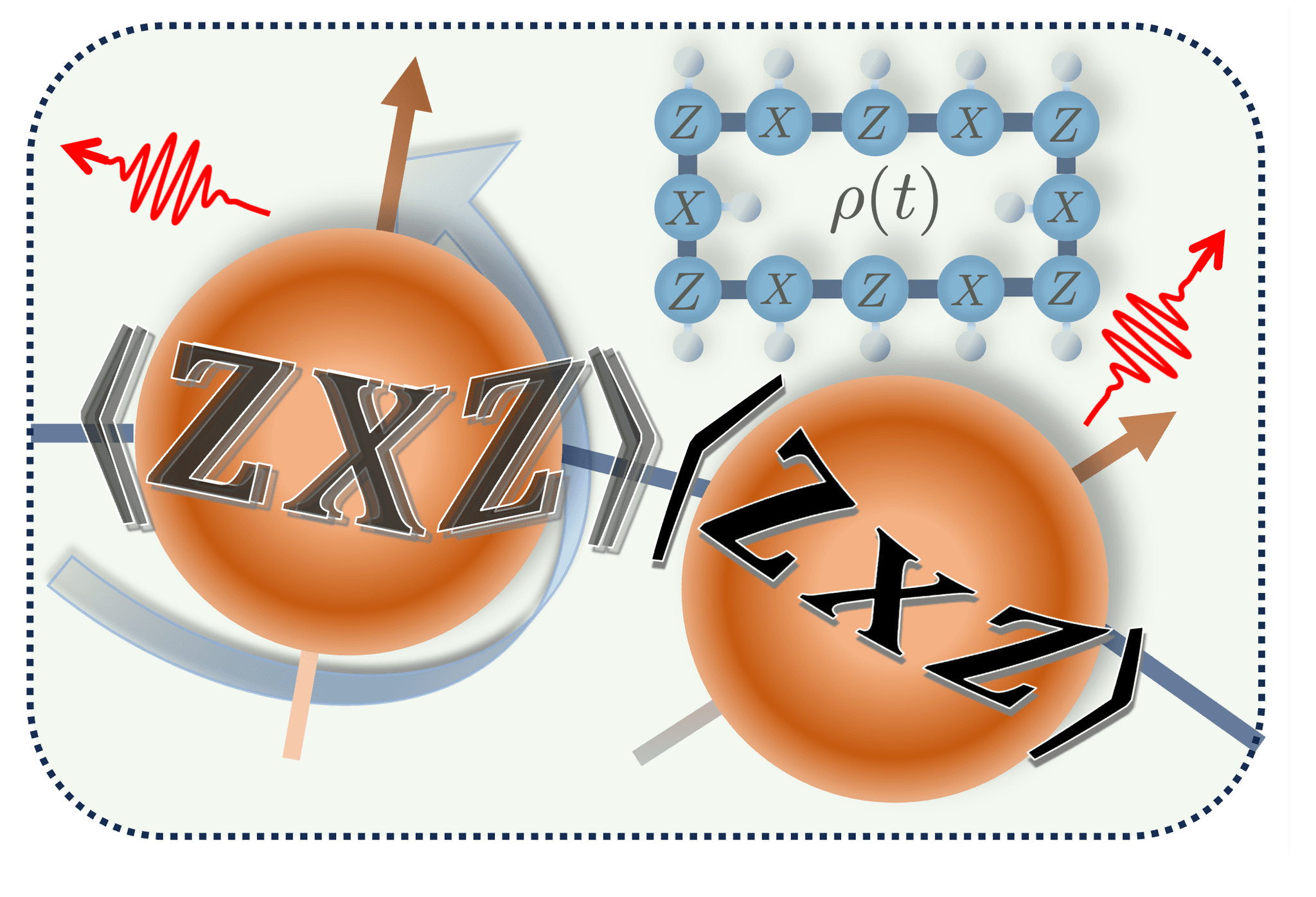
A schematic depiction of the ZXZ stabilizers of a graph state in a noisy environment. The quantum state is prepared on twelve qubits coupled to their neighbors on each side, as illustrated in the background along with a noise source for each qubit included in the dynamical model.
Modeling charge-parity fluctuations in many-body systems
The fact that stabilizers are multi-qubit observables is part of what makes them so powerful. They help us deal with quantum states and operations in more compact ways because they describe many qubits, not just one. At the same time, their multi-qubit nature also poses significant challenges when it comes to building accurate models of the noise that affects them.
As of today, there are no truly accurate noise models for the many-body regime of qubit dynamics—i.e., for noisy quantum states involving many qubits—though many researchers are working to build them. Our paper represents a promising step forward in that effort. One thing that sets our work apart from previous research in this field has to do with a special phenomenon that occurs in superconducting qubits, which is known as charge-parity splitting.
You can think of charge-parity in superconducting qubits as a measurable property that is determined by the number of charge-carrying particles that tunnel into and out of the qubit hardware. (Note: This is a highly simplified picture of reality.) In this context, charge-parity splitting refers to the way in which the frequency of each qubit depends on the number-parity of those charge carriers, i.e., whether the total number of charge carriers is even or odd. When the charge-parity fluctuates, it causes the qubit frequency to shift slightly across different experimental repetitions.
Properly accounting for these frequency shifts is essential for building a valid model of many-body qubit dynamics, but previous research has studied this problem only in the context of single-qubit experiments. Our research is the first to demonstrate an efficient method for modeling charge-parity fluctuations in many-body systems—including the systems of qubits we want to keep idle, which are subject to uncontrolled noise.
Our secret weapon: characterization experiments and dynamical simulations
We developed a classical simulation method that is efficient for modeling charge-parity noise in multi-qubit dynamics. To achieve this, it was important to ensure that our method was suitable for use with tensor-network approximations—powerful tools that help us simulate quantum systems classically by compressing the information needed to represent those systems.
In particular, we used lindbladmpo, a high-performance software tool for simulating continuous-time dynamics of noisy quantum systems with classical computation. The lindbladmpo solver was originally developed by our team together with our collaborator Grégoire Misguich in 2022, and uses tensor network approximations to store and manipulate the in-memory representation of multi-qubit states. This simulation method is particularly efficient for quantum states in which distant qubits are not too strongly correlated or entangled.
We won’t go into much more detail about lindbladmpo here. You can learn more about it in our previous Qiskit blog on the subject. In the context of this work, lindbladmpo allows us to accurately simulate the quantum state we are studying even with tens of qubits, which is impossible to achieve using other methods.
However, what connects these simulations to the real world is our use of Qiskit, and in particular Qiskit Experiments, to feed the simulations with relevant, up-to-date hardware parameters. Qiskit Experiments is a project from the Qiskit ecosystem. Readers can learn more about the ecosystem and check out other ecosystem projects that use or extend Qiskit by visiting the Qiskit ecosystem homepage.
Qiskit Experiments gives us a powerful and flexible framework for running characterization experiments. This framework greatly simplifies the process of probing various device parameters, analyzing and plotting the data, saving the results and figures, and even gives us the ability to automate all of that across large devices with hundreds of qubits.
For example, using Qiskit Experiments it is easy to run a T_1 characterization experiment on all or some of the qubits of the device, with the qubits divided into groups according to the desired parallelism. Below is some example code that would achieve this goal, with the plots and fit parameters seamlessly auto-generated for us. Note that, for simplicity’s sake, we assume the qubits' partition, the required time delays, and the backend we’ll run the experiment on have already been initialized, and that the Python imports have also been dropped:
T1_experiments = []
for group in all_qubits:
experiments = []
for qubits in group:
exp = T1(physical_qubits=qubits, delays=delays_T1)
experiments.append(exp)
parallel_exp = ParallelExperiment(experiments)
T1_experiments.append(parallel_exp)
final_exp = BatchExperiment(T1_experiments)
exp_data = final_exp.run(backend=backend)In our experiments, we run an extensive characterization of seven parameters per qubit that are needed for the dynamical model — six dissipative and coherent single-qubit parameters, and one two-qubit parameter denoting the strength of the coupling between the qubit and each of its neighbors. We also characterize five parameters per qubit to account for state preparation and readout errors. We estimate all of these hardware parameters for the individual qubits or qubit pairs in one set of experiment jobs, and then feed 10 of them (per qubit) into the simulations.
![(a) Our experiments focus on the dynamics of an open quantum system with a density matrix ρ(t) comprising 12 qubits in a ring. (b) The superconducting-qubit levels (with frequency ω) are split due to the charge-parity fluctuations shifting the qubit frequency by ± ν. (c) To model the charge-parity splitting in a many-body simulation, each qubit Q is coupled to a fictitious two-level system [with levels “e” (even) and “o” (odd)] initialized to a diagonal mixed state. The model further includes standard coherent and dissipative single-qubit noise terms and two-qubit ZZ crosstalk. gss-fig1.png](https://research-website-prod-cms-uploads.s3.us.cloud-object-storage.appdomain.cloud/gss_fig1_7fa02e3795.png)
(a) Our experiments focus on the dynamics of an open quantum system with a density matrix ρ(t) comprising 12 qubits in a ring. (b) The superconducting-qubit levels (with frequency ω) are split due to the charge-parity fluctuations shifting the qubit frequency by ± ν. (c) To model the charge-parity splitting in a many-body simulation, each qubit Q is coupled to a fictitious two-level system [with levels “e” (even) and “o” (odd)] initialized to a diagonal mixed state. The model further includes standard coherent and dissipative single-qubit noise terms and two-qubit ZZ crosstalk.
Qubits can also suffer from noise and fluctuations that our model cannot capture. However, in many cases, the simulations of the dynamics of complex entangled states are highly successful. We demonstrate this by comparing our simulations to stabilizers that are measured experimentally.
Applying these methods to future research
Using lindbladmpo, we found we were able to build remarkably accurate simulations of superconducting qubits’ idle dynamics, which tells us a lot of useful information about how individual stabilizers evolve over time. Moreover, we show that we can suppress a significant part of the coherent noise in the system using tailored techniques called dynamical decoupling, which we can also apply to remove two-qubit crosstalk.
The set of tools we’ve demonstrated in our research could very well represent a significant first step toward high-fidelity noise simulations that have the potential to be useful for quantum error correction. And we’re already working to take the next step along this path, which you can learn about in our latest preprint, here.
Our entire experiment and all the simulation software we used with it are available as open source resources here. Just check the repo’s README file for instructions on getting started. We encourage you to run your experiments on IBM Quantum processors, and use our model and simulations as a starting point to analyze quantum error correction and mitigation.
This research was supported by the QCISS program of the Army Research office (Grant Number W911NF-21-1-0002).



