The history of classical computing is one of advances in transistor and chip technology yielding corresponding gains in information processing performance. Although quantum computers have seen tremendous improvements in their scale, quality and speed in recent years, such a gradual evolution seems to be missing from the narrative. Indeed, it is widely accepted that one must first build a large fault-tolerant quantum processor before any of the quantum algorithms with proven super-polynomial speed-up can be implemented. Building such a processor therefore is the central goal for our development.
However, recent advances in techniques we refer to broadly as quantum error mitigation allow us to lay out a smoother path towards this goal. Along this path, advances in qubit coherence, gate fidelities, and speed immediately translate to measurable advantage in computation, akin to the steady progress historically observed with classical computers.
Of course, the ultimate litmus test for practical quantum computing is to provide an advantage over classical approaches for a useful problem. Such an advantage can take many forms, the most prominent one being a substantial improvement of a quantum algorithm’s runtime over the best classical approaches. For this to be possible, the algorithm should have an efficient representation as quantum circuits, and there should be no classical algorithm that can simulate these quantum circuits efficiently. This can only be achieved for specific kinds of problems.
Accessing a quantum advantage therefore requires us to answer two questions. First, which problems can we map to quantum circuits that have solutions which are better than classical approaches? Second, how can we obtain reliable outcomes for these circuits on quantum hardware with a faster runtime?
Addressing the first question is not something we can do alone. It is our commitment to work with the community and industry experts to find problems that are solvable with quantum circuits that are known to be difficult to simulate classically. This is the reason we have built the world’s largest quantum ecosystem with the IBM Quantum Network, made up of Fortune 500 companies, academic institutions, national entities, start-ups, and the Qiskit Community to explore the problem space of quantum circuits to drive real application and value.
How then do we chart a path to address the second question in practice?
Current quantum hardware is subject to different sources of noise, the most well-known being qubit decoherence, individual gate errors, and measurement errors. These errors limit the depth of the quantum circuit that we can implement. However, even for shallow circuits, noise can lead to faulty estimates. Fortunately, quantum error mitigation provides a collection of tools and methods that allow us to evaluate accurate expectation values from noisy, shallow depth quantum circuits, even before the introduction of fault tolerance.
In recent years, we developed1 and implemented two general-purpose error mitigation methods, called zero noise extrapolation (ZNE)2 and probabilistic error cancellation (PEC).3 The ZNE method cancels subsequent orders of the noise affecting the expectation value of a noisy quantum circuit by extrapolating measurement outcomes at different noise strength. More recently, theoretical and experimental advances have shown that PEC can already enable noise-free estimators of quantum circuits on noisy quantum computers.
In PEC, we learn and effectively invert the noise of the circuit of interest for the computation of expectation values by averaging randomly sampled instances of noisy circuits. The noise inversion, however, leads to pre-factors in the measured expectation values that translate into a circuit sampling overhead. This overhead is exponential in the number of qubits n and circuit depth d. The base of this exponential, represented as γ̄, is a property of the experimentally learned noise model and its inversion. We can therefore conveniently express the circuit sampling overhead as a quantum runtime, J:
J = γ̄ nd β d
Here, γ̄ is a powerful quality metric of quantum processors — in technical terms, γ̄ is a measure of the negativity of the quasi-probability distribution used to represent the inverse of the noise channel. Improvements in qubit coherence, gate fidelity and crosstalk will reflect in lower γ̄ values and consequently reduce the PEC runtime dramatically. Meanwhile, β is a measure of the time per circuit layer operation (see CLOPS),4 an important speed metric.
The above expression therefore highlights why the path to quantum advantage will be one driven by improvements in the quality and speed of quantum systems as their scale grows to tackle increasingly complex circuits. In recent years we have pushed the needle on all three fronts:
- We unveiled our 127-qubit Eagle processor, pushing the scale of these processors well beyond the boundaries of exact classical simulability.
- We also introduced a metric to quantify the speed of quantum systems — CLOPs — and demonstrated a 120x reduction in the runtime of a molecular simulation.
- The coherence times of our transmon qubits exceeded 1 ms, an incredible milestone for superconducting qubit technology.
- Since then, these improvements have extended to our largest processors, and our 65-qubit Hummingbird processors have seen a 2-3x improvement in coherence, which further enables higher fidelity gates.
- In our latest Falcon r10 processor, IBM Prague, two-qubit gate errors dipped under 0.1%, yet another first for superconducting quantum technology, allowing this processor to demonstrate two steps in Quantum Volume of 256 and 512.
These improvements in the quality of quantum processors have led to continually decreasing γ̄. Measured over the best 10-qubit strings on our large processors, here are some examples of the estimated γ̄:
| Improvements | γ̄ | |
|---|---|---|
| Hummingbird r2 (Brooklyn, 65Q) | 1.038 | |
| Hummingbird r3 (Ithaca, 65Q) | 2-3x coherence improvements over r2 | 1.024 |
| Falcon r10 (Prague, 32Q) | State-of-the-art two-qubit gates, reduced crosstalk | 1.012 |
Table 1: Comparing the γ̄ of three recent IBM Quantum processors
While these improvements in γ̄ might seem modest, it is important not to underestimate the power of exponentials. The run-time implications of these γ̄ improvements are huge — for instance, for a 100-qubit circuit of depth 100, the runtime overhead going from the quality of Hummingbird r2 to Falcon r10 is dramatically reduced by 110 orders of magnitude.
Let’s also look at a concrete example of how reductions in two-qubit gate errors will lead to dramatic improvements in quantum runtime. Consider the example of 100 qubit Trotter-type circuits of varying depth representing the evolution of an Ising spin chain. This is at a size well beyond exact classical simulation. In the figure below we estimate the PEC circuit overhead as a function of two-qubit gate error.
As discussed above, two-qubit gate errors on our processors have recently dipped below 1e-3. This suggests that if we could further reduce our gate error down to ~ 2-3e-4, we could have access to noise-free observables of 100 qubit, depth 400 circuits in less than a day of runtime. Furthermore, this runtime will be reduced even further as we simultaneously improve the speed of our quantum systems.
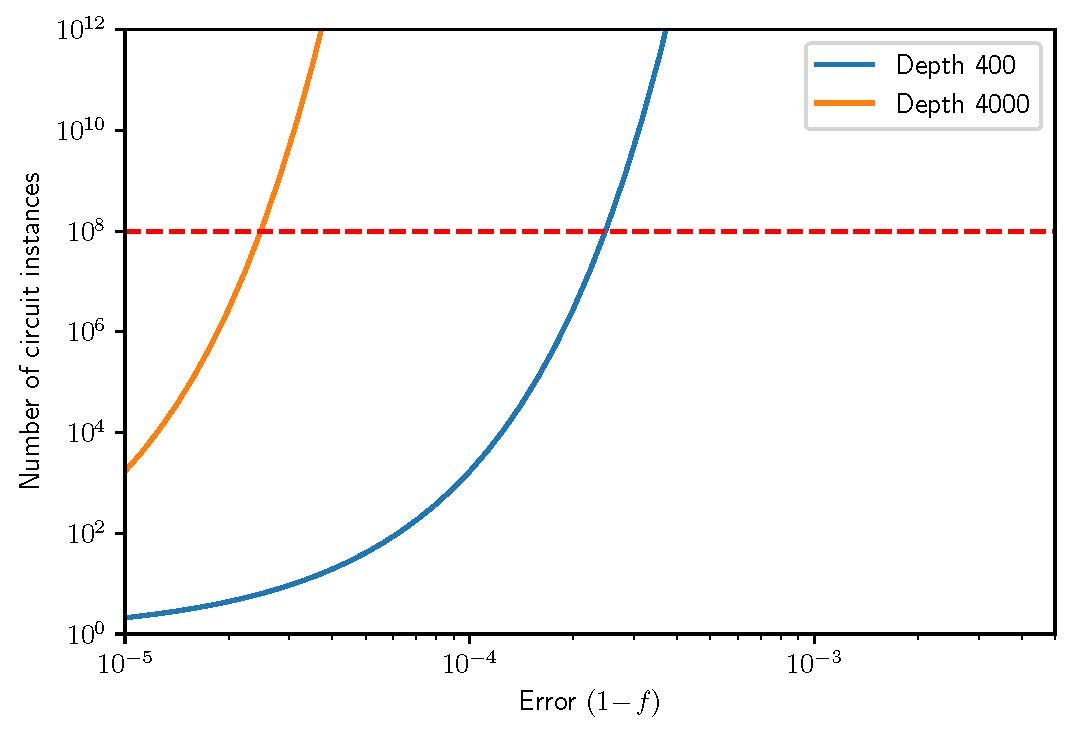
Fig. 1: Estimating the PEC circuit overhead for 100 qubit trotterization circuits of depth 400 and 4000, representing the time evolution of an Ising spin chain. Dotted red line indicates 1 day of runtime assuming a fixed 1kHz sampling rate.
We can therefore think of our proposed path to practical quantum computing as a game of exponentials. Despite the exponential cost of PEC, this framework, and the mathematical guarantees on the accuracy of error mitigated expectation values, allow us to lay down a concrete path and a metric (γ̄) to quantify when even noisy processors can achieve computational advantage over classical machines. The metrics γ̄ and β provide numerical criteria for when the runtime of quantum circuits will outperform classical methods that produce accurate expectation values, even before the advent of fault tolerant quantum computation.
To understand this better, let us consider the example of a specific circuit family: hardware-efficient circuits with layers of Clifford entangling gates and arbitrary single-qubit gates. These circuits are extremely relevant for a host of applications ranging from chemistry to machine learning. The table below compares the runtime scaling of PEC with the runtime scaling of the best classical circuit simulation methods, and estimates the γ̄ required for error mitigated quantum computation to be competitive with best-known classical techniques.
| Algorithm | Runtime in seconds (n=d) | Competitive boundary |
|---|---|---|
| Full state-vector (Orion) | (5*10-13)*n2 x 2n | γ̄ < 1.01 @ 56 qubits |
| Leading classical method5 | (1*10-5)*(1.262)n | γ̄ < 1.003 @ 100 qubits |
Table 2: Competitive boundary at which quantum processors error-mitigated with PEC are expected to outperform the corresponding classical algorithm
Improvements in qubit coherence time or better gate fidelities lower the metric γ̄. Faster circuit execution provides a smaller β. These advances then translate into larger circuit volumes that can be run on the noisy hardware while still producing superior expectation values.
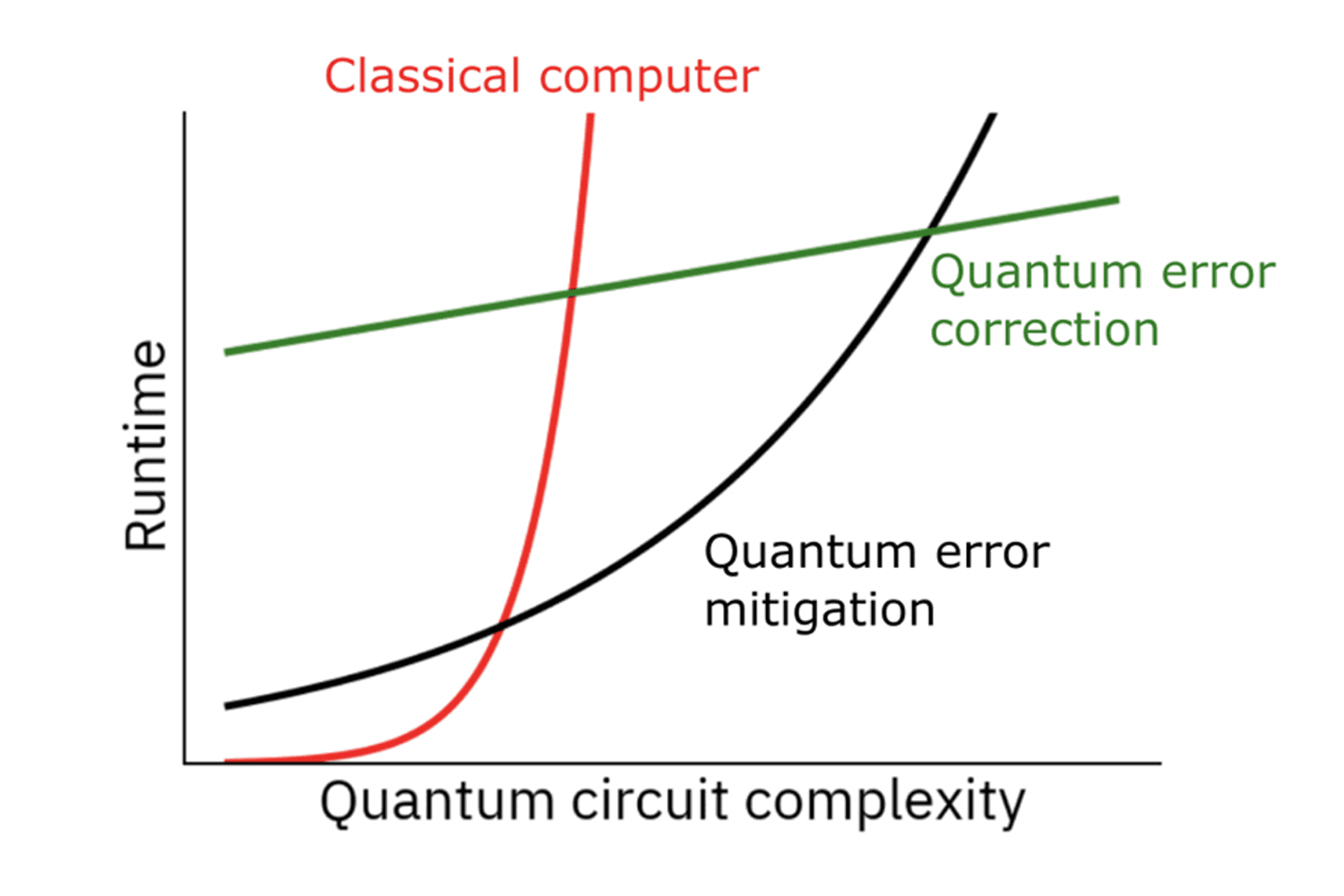
Fig. 2: Charting quantum runtime as a function of quantum circuit complexity for classical computers, quantum computers with error correction, and quantum computers with error mitigation. Quantum error mitigation will fill the gap before QEC achieves practical runtime reductions.
Ongoing research into the combination of error-mitigation methods with error correction techniques can be interpreted as the lowering of an effective γ̄ for the quantum circuits, as explored for example in Error Mitigation for Universal Gates on Encoded Qubits.6 These advances improve γ̄ up until the advent of fully fault tolerant quantum computing. At this point, the exponential scaling turns in to the polynomial overhead ensured by the threshold theorem.
These ideas go beyond just theory; we’ve already started to demonstrate the efficacy of error mitigation on large processors. Building upon recent work,3 we consider 50-qubit circuits with two layers of CNOT gates (equivalent to an identity operation) and measure Z stabilizers of increasing weight. In the absence of noise, the expectation values are +1, but decoherence, gate errors, and measurement errors heavily bias the accuracy of the observables, particularly with increasing weight. With error mitigation, we are able to show a remarkable improvement in the accuracy of these observables. A particular highlight is the contrast in the highest-weight observables before and after error mitigation, serving as a powerful example of trading run-time for extracting noise-free information about the state.
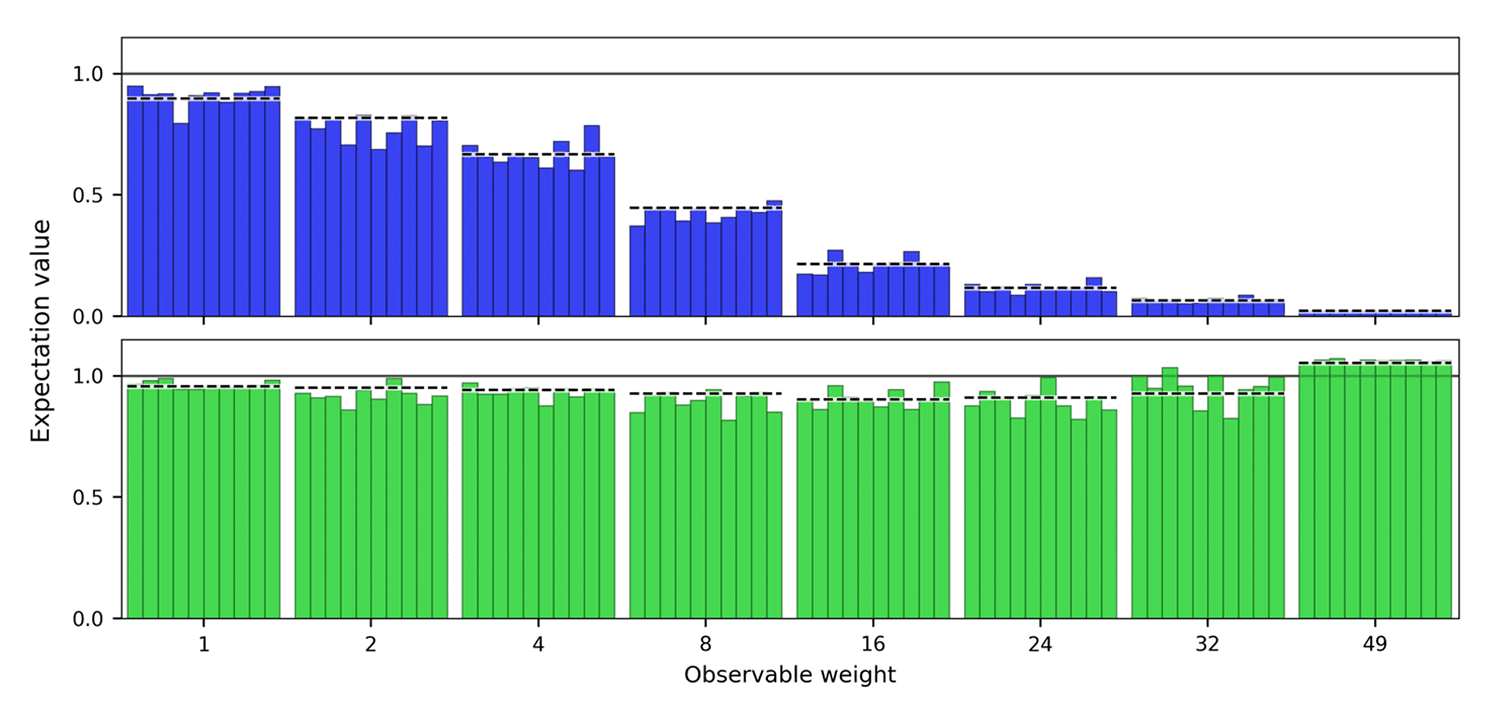
Fig. 3: Increasing weight observables before and after error mitigation on 50-qubit identity equivalent circuits with two layers of CNOT gates. For all weights the noise-free expectation value should be equal to 1. Before error mitigation, the high weight observables are increasingly biased from the ideal value due to errors. Error mitigation recovers the expectation values.
In a second example we go beyond the identity-equivalent circuits, and prepare strongly entangled graph states on 36 qubits. Even here, we demonstrate a remarkable recovery in the accuracy of the error-mitigated stabilizers, particularly at large weight.
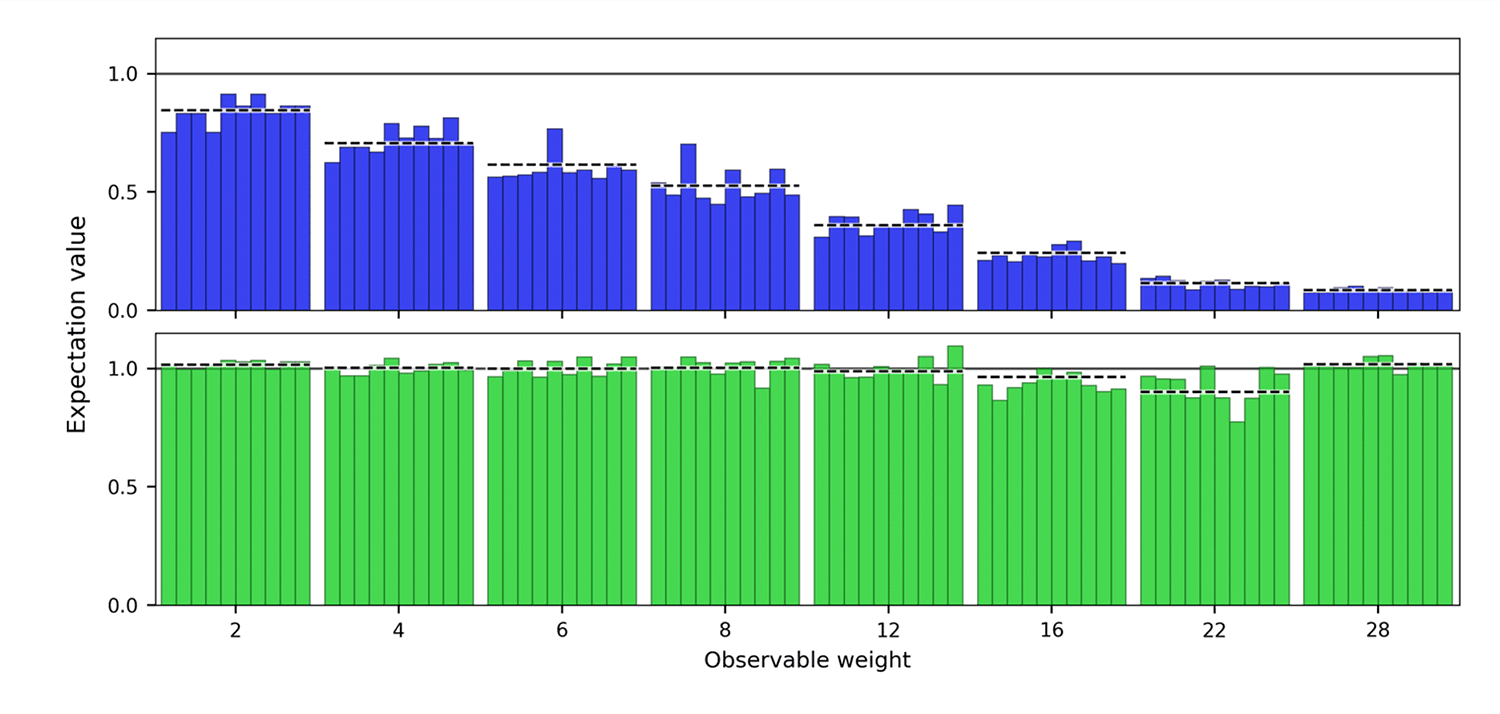
Fig. 4: Increasing weight observables before and after error mitigation on 36-qubit graph state circuits. For all weights the noise-free expectation value should be equal to 1. Before error mitigation, the high weight observables are increasingly biased from the ideal value due to errors. Error mitigation recovers the expectation values.
These examples illustrate the power of error-mitigation techniques, and show that these techniques continue to work even as the number of qubits increases towards the limit of exact classical simulability.
The ability of PEC to produce noise-free estimators enables clean runtime comparisons with exact classical simulations. We must contrast this with heuristic classical quantum simulation methods that may produce approximations in specific settings. We know of many such heuristics which, in some limit, produce correct expectation values, as is the case for tensor network methods that achieve accuracy in a large bond dimension limit, for example.
Such approximation methods are more suitably compared to error mitigation techniques such as ZNE, which provide biased estimators. The ZNE estimator can provide valuable approximations to the expectation value for low noise rates, and can be progressively improved by increasing the order of the extrapolation. This estimator significantly reduces run-time compared to a full PEC implementation.
The ZNE method was first demonstrated7 for studying the ground state energies of small molecules. More recently, we extended the method8 to even larger system sizes (up to 26 qubits) and observed that the time evolution of certain error mitigated observables was competitive with respect to approximate tensor-network based classical methods such as Projected Entangled Pair States (PEPS).
In order to weigh such heuristics against error mitigation methods like ZNE, we can contrast the expense of one resource to one that is relevant to the hardware implementation. For instance, contrast increased computation time for higher bond dimensions to the noise rate of the processor. This places us in the fortuitous situation where we can access computational advantage via certifiably accurate expectation values by employing PEC at the runtime expense discussed here, or by choosing a biased estimator from ZNE with an even lower runtime.
At IBM Quantum, we plan to continue developing our hardware and software with this path in mind. As we improve the scale, quality, and speed of our systems, we expect to see decreases in γ̄ and β resulting in improvements in quantum runtime for circuits of interest.
At the same time, together with our partners and the growing quantum community, we will continue expanding the list of problems that we can map to quantum circuits and develop better ways of comparing quantum circuit approaches to traditional classical methods to determine if a problem can demonstrate quantum advantage. We fully expect that this continuous path that we have outlined will bring us practical quantum computing.