| Overview | Group | Tree | Graph | Deprecated | Index | Concepts |
| Precedence constraints |
| Logical constraints |
This section describes common constraints in scheduling, namely, precedence constraints.
Informally, these constraints restrict the relative position of interval variables in a
solution. For instance a precedence constraint can model the fact that an activity a must
end before activity b starts (optionally with some minimum delay z). If one or both of the
interval variables of the precedence constraint is absent, then the precedence is systematically
considered to be true, and, thus, it does not impact the schedule.
More formally, the semantics of the relation TC(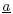 ,
,
 , z) on a pair of fixed intervals a, b and
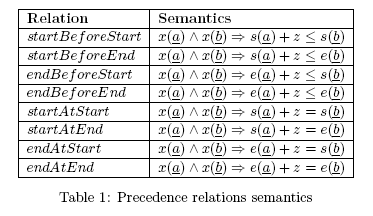
for a value z depending on the constraint type TC is given in Table 1.
, z) on a pair of fixed intervals a, b and
for a value z depending on the constraint type TC is given in Table 1.
Presence status of interval variables can be further restricted by logical constraints. The
presence constraint presenceOf(a) states that a given interval variable must be present.
Of course, this constraint may be used in logical constraints; for example, there may be two
optional intervals a and b, but if interval a is present
then b must be present too. This can be
modeled by the constraint presenceOf(a)  presenceOf(b).
presenceOf(b).
The semantics of the presence constraint on a fixed interval 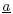 is just:
is just:
presenceOf(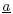 )
)  x(
x(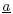 )
)