| Overview | Group | Tree | Graph | Deprecated | Index | Concepts |
| Semantics |
| OPL formulation |
| Examples |
This section describes the isomorphism constraint between two sets of interval variables.
In the same manner that the inverse constraint constrains two arrays of integer variables, the isomorphism constraint constrains two arrays of interval variables. The isomorphism constraint "synchronizes" the presence of each index pair of interval variables in the two arrays.The isomorphism constraint is used when a set of operations is subject to two independent scheduling models.
For example:
Consider two sets of interval variables,
A= and B=
and B= .
This constraint states that, in a solution, there is
a 1-to-1 correspondence between the present intervals of A and the present intervals of B; two
intervals in correspondence have the same start and end values. The isomorphism constraint
is useful to enforce some patterns of constraints on a set of interval variables (see the example
blelow).
.
This constraint states that, in a solution, there is
a 1-to-1 correspondence between the present intervals of A and the present intervals of B; two
intervals in correspondence have the same start and end values. The isomorphism constraint
is useful to enforce some patterns of constraints on a set of interval variables (see the example
blelow).
More formally, let P(A) = {a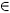 A, x(
A, x(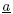 )=1}
and P(B) = {b
)=1}
and P(B) = {b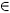 B, x(
B, x( )=1}.
The isomorphism constraint isomorphic(A,B) holds if and only if:
)=1}.
The isomorphism constraint isomorphic(A,B) holds if and only if:

The constraint can be passed an additional set of |A| integer variables V= with domain in [0, |B|
with domain in [0, |B| {
{ }] that describes the bijective function
f at the solution: the constraint isomorphic(A,B,F) holds if and only if:
}] that describes the bijective function
f at the solution: the constraint isomorphic(A,B,F) holds if and only if:

In other words, V is an indexer that gives the position of a present interval in A, as an ordered set, of its corresponding present interval in B, as an ordered set. The position of
an absent interval of A is, by convention, set to  .
.
The isomorphism constraint is illustrated in the figure.

The construct below is a constraint:
isomorphism(A, B [, F, eps]);
where
dvar interval A[]; // Array of size n dvar interval B[]; // Array of size n dvar int V[]; // Array of size n int eps; // Integer Escape Value
Important: The constraint isomorphism cannot be used in logical constraints.
A set of n activities a[1],...,a[n] is to be sequenced on a worker,
each activity a[i] has a nominal duration NDur[i]. There is a position-based learning
effect: as the worker is executing the activities, it is learning so that if activity a[i] is
executed in position j in the sequence, its actual duration will be
max (NDur[i], 2 x NDur[i] x ) where
) where

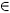 [0,1] is the learning index.
Other components of the problem are that each task
cannot start before its release date, can be delayed from its tardiness date against a
linear cost and is eventually abandoned for a cost of NDur[i].
[0,1] is the learning index.
Other components of the problem are that each task
cannot start before its release date, can be delayed from its tardiness date against a
linear cost and is eventually abandoned for a cost of NDur[i].
Besides the n real activities a[i] modeled as interval variables, the model below
introduces a chain of slots s[j] on the worker that represents the sequence of activities
of the worker. Slot intervals s[j] will give the position of the jth activity executed
by the worker. The mapping between the two sets of intervals is achieved by using an
isomorphism constraint.
int n = ...; // Number of activities
float alpha = ...; // Learning factor in [0, 1]
int NDur[i in 1..n] = ...; // Nominal duration
int Rd[i in 1..n] = ...; // start date release date
int Dd[i in 1..n] = ...; // end date tardy date
dvar interval a[i in 1..n] optional; // Real activities
dvar interval s[j in 1..n] optional; // Consecutive slots on machine
dvar int p[i in 1..n] in 1..n; // Mapping slot and activity
minimize sum(i in 1..n) maxl(0, endOf(a[i], 2*Dd[i]) - Dd[i]);
subject to {
noOverlap(a);
isomorphism(s,a,p,0); // 0: position for absent activity
forall (i in 1..n-1) {
endBeforeStart(a[i+1], a[i]);
presenceOf(a[i + 1]) <= presenceOf(a[i]);
}
forall (i in 1..n) {
startOf(a[i], Rd[i]) >= Rd[i];
sizeOf(a[i], NDur[i])== maxl(NDur[i],
ftoi(round(2*NDur[i]*pow(alpha,p[i]))));
}
}