| Overview | Group | Tree | Graph | Deprecated | Index | Concepts |
The class IlcFloatExp is the root for constrained
floating-point expressions. A constrained floating-point expression computes
its domain from the domains of its subexpressions.
In fact, a constrained floating-point variable itself is a
constrained floating-point expression: the class
IlcFloatVar is a subclass of IlcFloatExp, so a
constrained floating-point variable is simply a constrained floating-point
expression whose domain is stored. Since the number of elements in the
domain of a constrained continuous floating-point variable is very high
(typically millions), there is usually an interval associated with
the variable to represent its domain.
Most member functions in this class contain assert
statements. For an explanation of the macro NDEBUG (a way to
turn on or turn off these assert statements), see the concept
Assert and NDEBUG.
Precision
In CP Optimizer, all computations on floating-point values are computed in double precision mode, that is, 64 bits on most hardware.
A relative precision is associated with each
constrained floating-point expression in CP Optimizer. This relative precision is
taken into account during constraint propagation: if the size of the
interval associated with a floating-point expression is less than the
precision associated with that expression, then we consider the expression
as fixed to the mean value in that interval. In other words, the expression
is fixed to the average value in a such an interval. Consequently, in this
context, precision represents a degree of uncertainty about this value. More
formally, we say that a constrained floating-point variable x
with a precision indicated by precision is fixed when
its associated interval is bounded by min and max
such that ((max - min)/(max{1, |min|}) <= precision.
The smaller the precision of a variable, the more precise are computations with it, but such computations can take more time, of course.
Domain
The domain of a constrained floating-point expression (an instance of
IlcFloatExp) is computed from the domains of its
subexpressions. For example, if x and y are both
instances of IlcFloatExp, then the domain of x+y
contains the range [x.getMin()+y.getMin(),
x.getMax()+y.getMax()]. (In contrast, the domain of a constrained
floating-point variable (an instance of IlcFloatVar) is
stored.) The domain of a constrained floating-point expression can be
reduced to the point of being empty. In such a case, failure is
triggered since no solution is then possible.
Checking Overflow and Underflow
CP Optimizer explicitly checks floating-point computations for overflow and underflow.
IEEE 754 is a standard proposed by the Institute of Electrical and Electronics Engineers, Inc. for computing floating-point arithmetic. The implementation of floating-point numbers in CP Optimizer conforms to this standard.
Backtracking and Reversibility
All the member functions and operators defined for this class and capable of modifying constrained variables are reversible. In particular, the changes made by constraint-posting functions are made with reversible assignments. Thus, the value, the domain, and the constraints posted on any constrained variable are restored when CP Optimizer backtracks.
For more information, see the concept Propagation in CP Optimizer.
A modifier is a member function that reduces the domain of a constrained floating-point expression, if it can. The modifier is not stored, in contrast to a constraint. If the constrained floating-point expression is a constrained floating-point variable, the modifications due to the modifier call are stored in its domain. Otherwise, the effect of the modifier is propagated to the subexpressions of the constrained floating-point expression. If the domain becomes empty, failure occurs. Modifiers are usually used to define new classes of constraints.
See Also:
IlcAbs, IlcFloatVar, IlcMax, IlcMin, IlcSquare, operator+, operator-, operator*, operator/, operator<<
| Method Summary | |
|---|---|
public void | display(ostream & str) const |
public IlcFloat | getMax() const |
public IlcFloat | getMin() const |
public IlcFloat | getPrecision() const |
public IlcFloat | getSize() const |
public | IlcFloatExp(IlcIntExp exp) |
public IlcBool | isFixed() const |
public IlcBool | isInDomain(IlcFloat value) const |
public void | setMax(IlcFloat max) const |
public void | setMin(IlcFloat min) const |
public void | setPrecision(IlcFloat p) const |
public void | setRange(IlcFloat min, IlcFloat max) const |
| Method Detail |
|---|
A constrained integer expression in CP Optimizer can be seen as a constrained floating-point
expression since integers can be converted to floating-point values. This constructor is
for casting a constrained integer expression into a constrained floating-point expression.
This constructor creates a constrained floating-point expression which is constrained to be
equal to the constrained integer expression exp. In other words, you can use
this constructor to define a constrained floating-point expression to be equal to a constrained
integer expression. Such a floating-point expression can then be used like any other constrained
floating-point expression. It is thus possible to combine integers and floating-point expressions
within a constraint.
Usually, casting a constrained integer expression to a constrained floating-point expression is done automatically by the compiler, so you should not need to use this constructor. You should use it only if your compiler warns you that something is wrong when you combine constrained floating-point and integer expressions.
This member function puts the invoking object on the output stream indicated by its argument.
This member function returns the maximum value of the invoking object.
This member function returns the minimum value of the invoking object.
This member function returns the precision of the invoking constrained floating-point
expression. We say that a constrained floating-point variable x with a precision
indicated by precision is fixed when its associated interval is bounded
by min and max such that 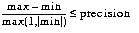
The smaller the precision of a variable, the more precise are computations with it, but such computations can take more time, of course.
This member function returns the width of the domain of the invoking constrained floating-point expression. By width of the domain, we mean the difference between the two boundaries of the domain.
This member function returns IlcTrue if the invoking constrained floating-point
expression is fixed to a value. Otherwise, the member function returns IlcFalse.
This member function returns IlcTrue if value is in the domain of
the invoking constrained floating-point expression. Otherwise, the member function returns IlcFalse.
This member function removes all the elements that are greater than max from
the domain of the invoking constrained expression. If the domain thus becomes empty, then the
function IlcFail is called. Otherwise, if the domain is modified, the propagation
event range is generated. Moreover, if the invoking constrained floating-point
expression becomes fixed, then the propagation event value is also generated.
The effects of this member function are reversible.
This member function removes all the elements that are less than min from
the domain of the invoking constrained expression. If the domain thus becomes empty, then t
he function IlcFail is called. Otherwise, if the domain is modified, the propagation
event range is generated. Moreover, if the invoking constrained floating-point
expression becomes fixed, then the propagation event value is also generated.
The effects of this member function are reversible.
This member function sets the precision of the invoking constrained floating-point expression. This is a non-reversible action.
This member function removes all the elements that are either less than min or
greater than max from the domain of the invoking constrained expression. If the
domain thus becomes empty, then a failure occurs. Otherwise, if the
domain is modified, the propagation event range is generated. Moreover, if the
invoking constrained floating-point expression becomes fixed, then the propagation event
value is also generated. The effects of this member function are reversible.