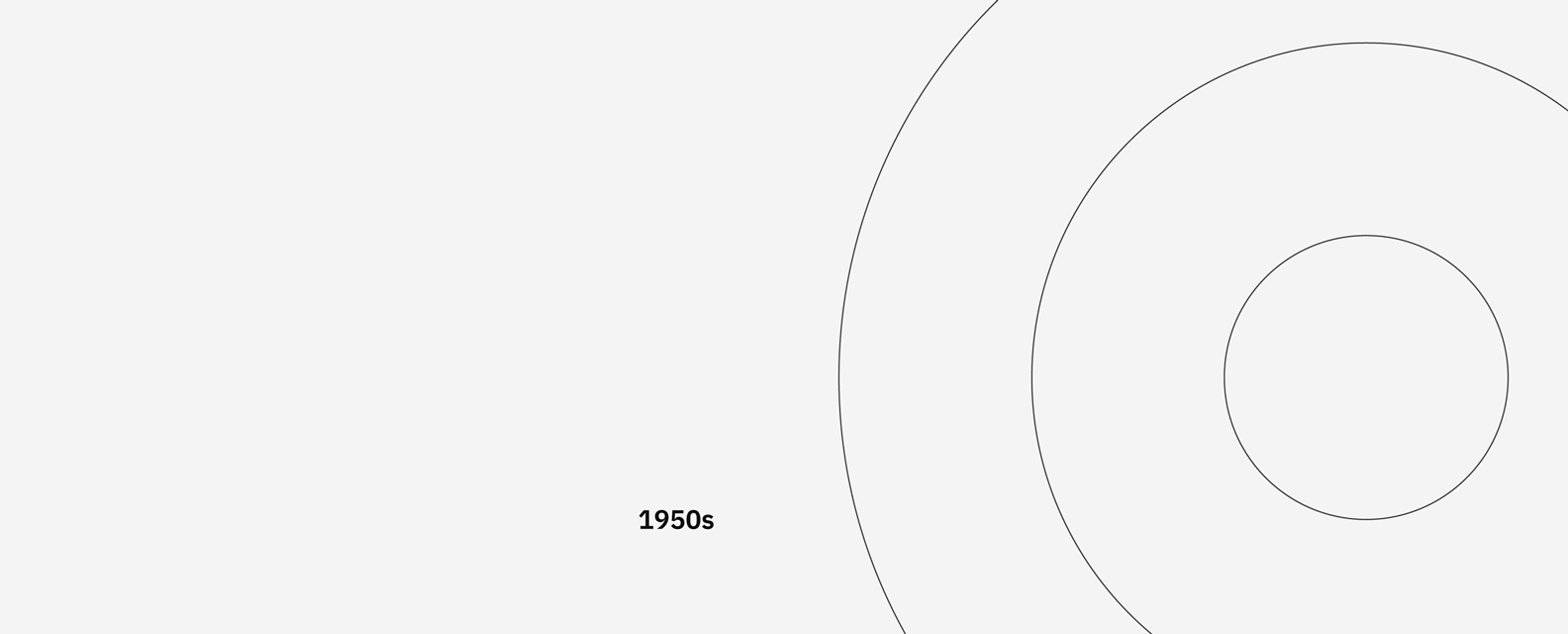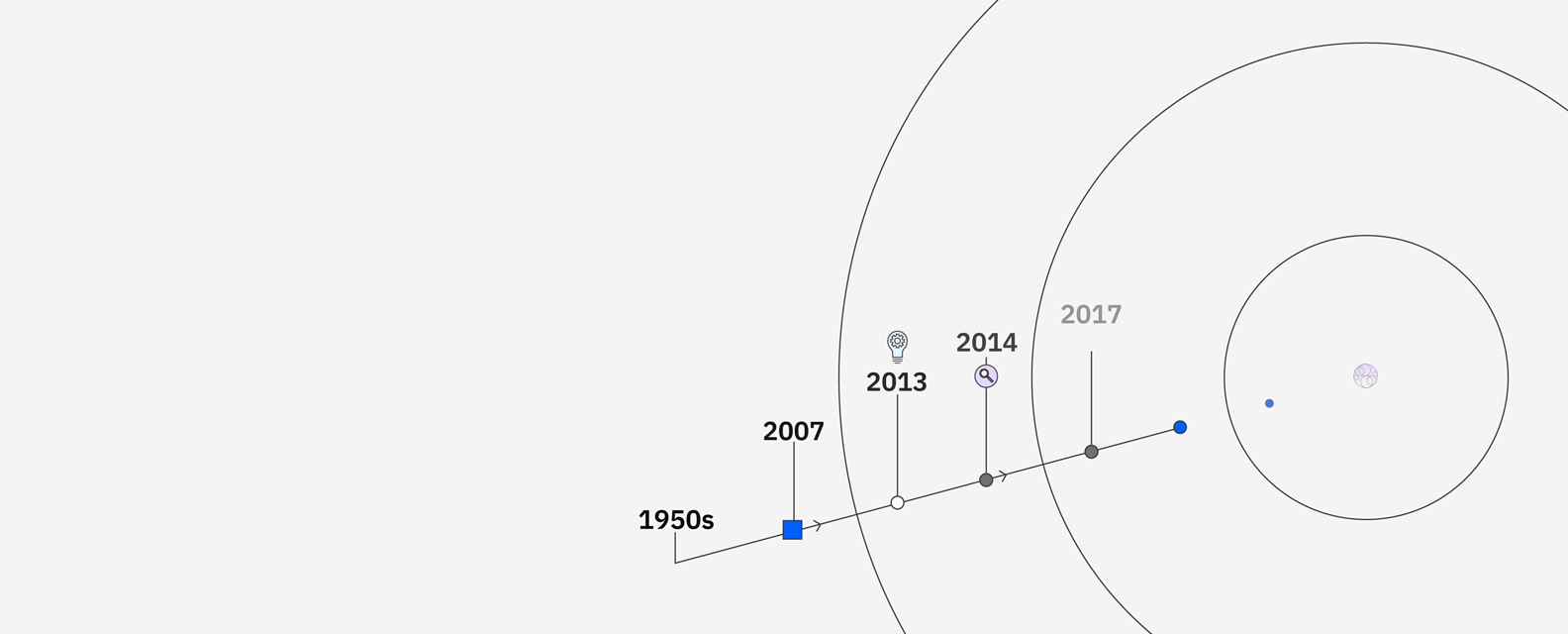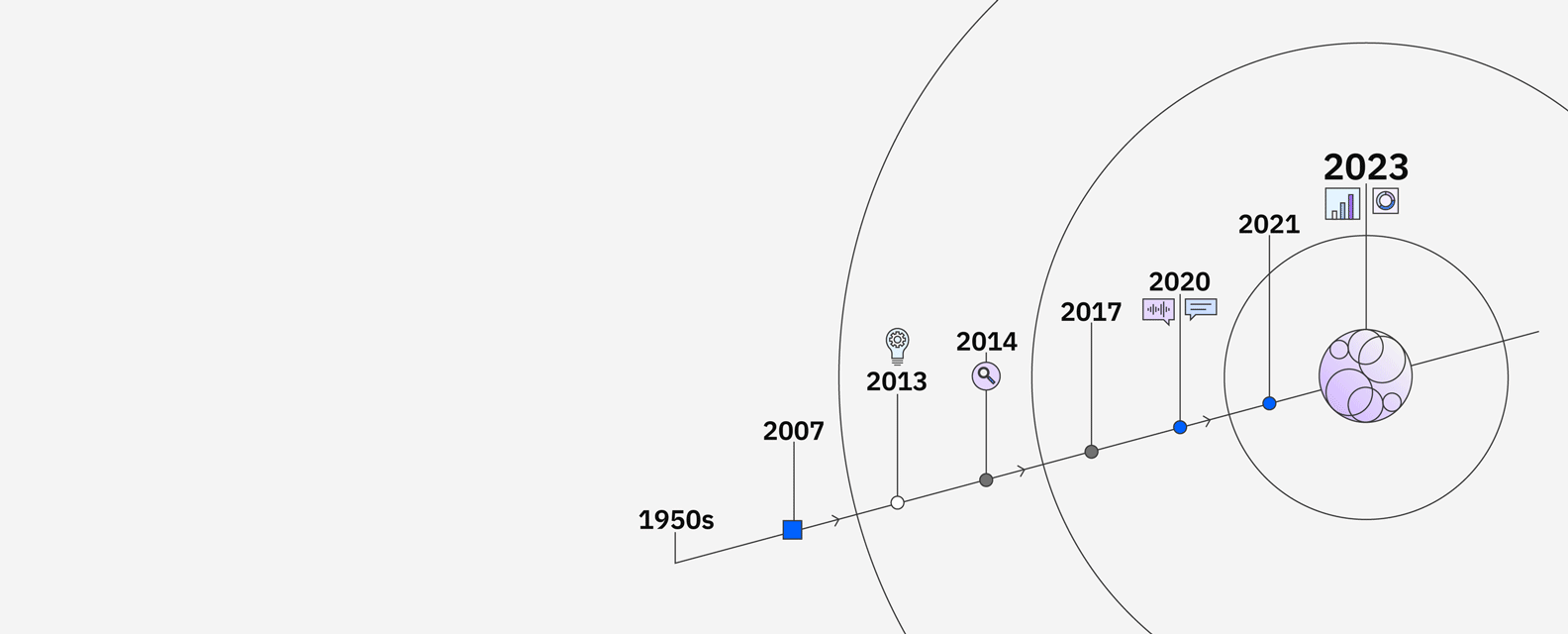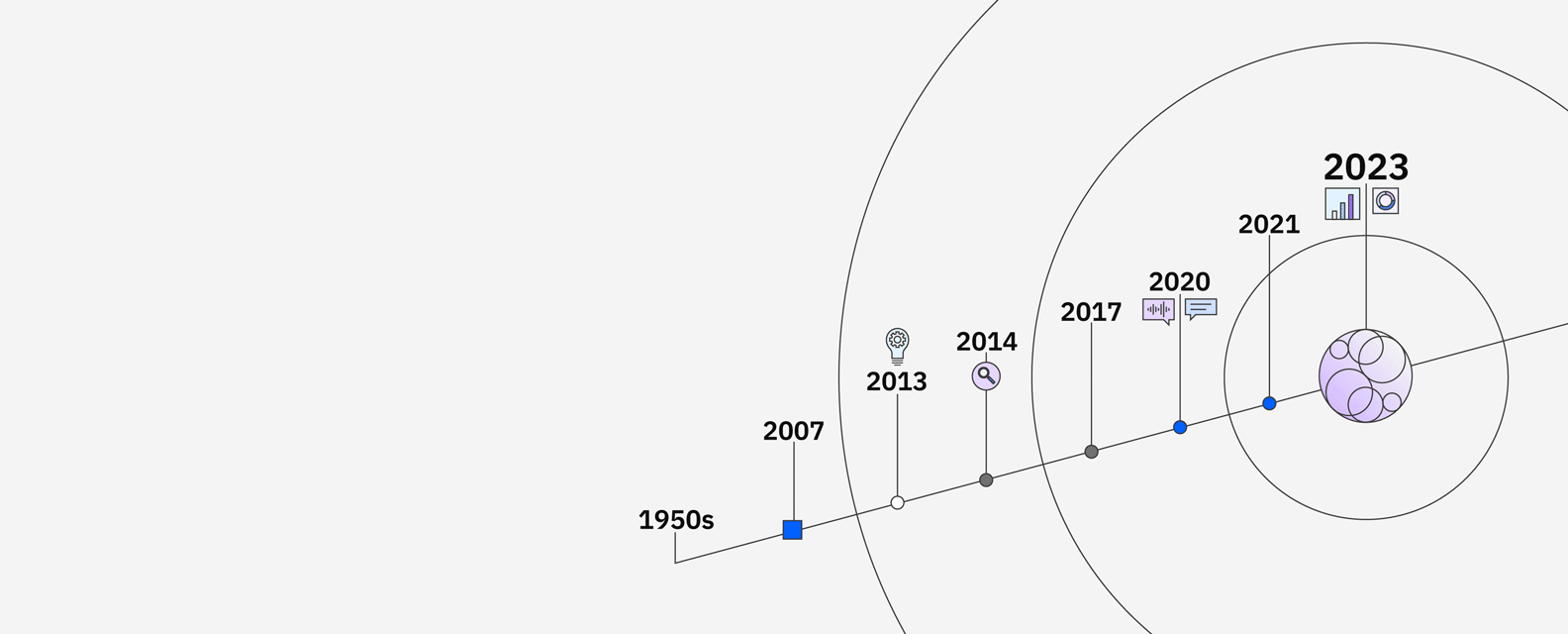
IBM’s research in AI goes back to the 1950s and includes significant milestones like the supercomputer Deep Blue defeating chess grandmaster Garry Kasparov. In 2011, IBM Watson defeated Brad Rutter and Ken Jennings in the Jeopardy! Challenge. To find and understand the clues in the questions, Watson compared possible answers by ranking its confidence in their accuracy, and responded — all in under three seconds.
Watson sparked curiosity around “machines that could think” and opened up the possibilities around how AI could be applied to business. Clients in industries ranging from financial services to retail put Watson to work to unlock new insights, drive productivity and deliver better customer experiences. Now through advancements in core Watson technologies, IBM has developed the next generation AI and data platform and set of AI assistants with watsonx.
Accelerate responsible, transparent and explainable workflows for generative AI built on third-party platforms
Train, validate, tune, and deploy foundation and machine learning models with ease.
Scale AI workloads, for all your data, anywhere.
Accelerate responsible, transparent and explainable data and AI workflows.
Empower everyone in the organization to build and deploy AI-powered virtual agents without writing a line of code.
Enable employees to quickly offload time-consuming work to tackle more of the work only they can do.
Empower developers of all experience levels to write code with AI-generated recommendations.